Gist
Synonymous with "variance components models, random-coefficients models and random-effects"
Importance
If there's a hierarchal structure in your data, it may violate the independence assumption of the observations. For example, student data collected from one school maybe more correlated to each other than the students collected in another school.
We're interested in it to separate between-group effects from within-group effects.
Also a good option for dealing with Longitudinal Data
Mathematics
Random intercept model
Given individual i j
You can't use 'macro parameter character #' in math mode y_{ij} = B_0 + B_1t_{ij} + \epsilon.$$Both the outcome variable ($y$) and the time variable ($t$) are allowed to vary by individuals and event. Note, that $\epsilon$ is the error term and we assume that it is normally distributed. We can modify the above equation using the random intercept model: $$ y_{ij} = B_0 + B_1t_{ij} +v_{0i} + \epsilon, $$where $v_{0i}$ is the individual-level effect which allows the subject to deviate from the overall mean response. The deviation is parallel- note that the slopes are all the same [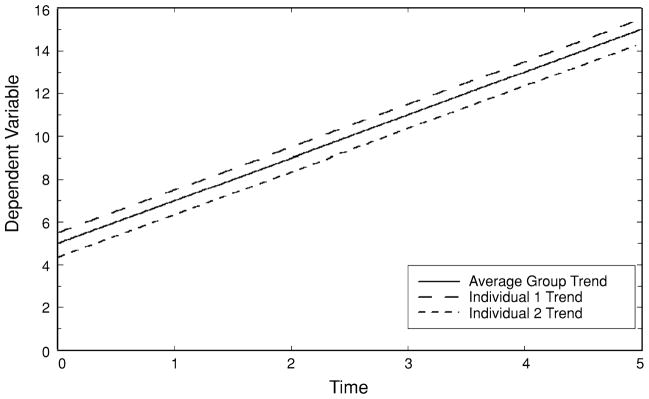](https://www.ncbi.nlm.nih.gov/core/lw/2.0/html/tileshop_pmc/tileshop_pmc_inline.html?title=Click%20on%20image%20to%20zoom&p=PMC3&id=2971698_nihms236714f1.jpg) #### Properties 1. "...Quite robust to missing data and irregularly spaced measurement occasions" ^[2] ### Reference 1. https://kenbenoit.net/assets/courses/mlm2011/MLM_day1.pdf 2. Gibbons RD, Hedeker D, DuToit S. Advances in analysis of longitudinal data. Annu Rev Clin Psychol. 2010;6:79-107. doi: 10.1146/annurev.clinpsy.032408.153550. PMID: 20192796; PMCID: PMC2971698. y_{ij} = B_0 + B_1t_{ij} + \epsilon.$$Both the outcome variable ($y$) and the time variable ($t$) are allowed to vary by individuals and event. Note, that $\epsilon$ is the error term and we assume that it is normally distributed. We can modify the above equation using the random intercept model: $$ y_{ij} = B_0 + B_1t_{ij} +v_{0i} + \epsilon, $$where $v_{0i}$ is the individual-level effect which allows the subject to deviate from the overall mean response. The deviation is parallel- note that the slopes are all the same [](https://www.ncbi.nlm.nih.gov/core/lw/2.0/html/tileshop_pmc/tileshop_pmc_inline.html?title=Click%20on%20image%20to%20zoom&p=PMC3&id=2971698_nihms236714f1.jpg) #### Properties 1. "...Quite robust to missing data and irregularly spaced measurement occasions" ^[2] ### Reference 1. https://kenbenoit.net/assets/courses/mlm2011/MLM_day1.pdf 2. Gibbons RD, Hedeker D, DuToit S. Advances in analysis of longitudinal data. Annu Rev Clin Psychol. 2010;6:79-107. doi: 10.1146/annurev.clinpsy.032408.153550. PMID: 20192796; PMCID: PMC2971698.